Hess' Law
- Saren

- May 6, 2020
- 3 min read
Hello everyone! Thanks for checking out this post on Hess' Law. Get ready for some math (not difficult math but math none-the-less.)
Why you should understand Hess' Law:
Key Ideas
- Defining Hess' Law
- Examples
- Summary
Defining Hess' Law
Hess' Law is a useful tool that chemists use to calculate the overall enthalpy of a reaction by using known enthalpy values for different reactions. Why would we need to do this? Because new reactions are discovered all the time. Sometimes, we don't know the specific enthalpy associated with one reaction, but we know other reactions. Also, it simply seems to be a right of passage for chemists, like some kind of cruel hazing. Whatever the reason, your professor has asked you to learn Hess' Law, so here I am teaching it to you.

First, look through these rules to the left. It's ok if they don't make complete sense right now, because I'm going to walk through the rules and 2 Hess' Law problems below.
Examples
Problem 1:
I start with the reaction below which has an enthalpy of -340 Kj/mol. We want to manipulate the starting reaction so it ends up looking like the second reaction.
1st - Switch the products and the reactants.
See how in the first equation the C is on the products side? In the second equation, it's on the reaction side. In our rules above, switching the products and reactants means that we must also switch the sign of the enthalpy. This causes our enthalpy to become 340 Kj/mol.
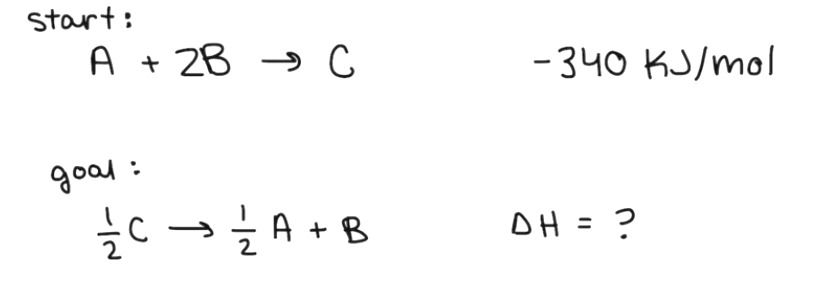
2nd - Multiply the flipped equation by one half.
In the second equation, the "B" term doesn't have a coefficient (number) in front of it. However, in the first equation, it has a 2. The "C" and "A" terms also have one-half coefficients in front of them. This means we must multiply the first equation by one half after we've flipped it. Our rules state that if we multiply the equation by a number then we also have to multiply the enthalpy value by that number. So half of 340 Kj/mol is 170 Kj/mol.
****Note: these two steps can be done in either order.
Problem 2:
Now we've got two equations which makes things a bit more tricker. I'm going to give you the steps which would solve this example, but I encourage you to try and solve it on your own using the rules above.
1st - Switch the products and reactants of the second equation.
The first thing I notice is that there are C's in both of the equations but no C's in the final equation. To cancel out the C's, they need to be on opposite sides of the equations from each other. Switching the second equation will also get the A terms on the correct side of the equation. The enthalpy for the first reaction remains as 24 Kj/mol. The enthalpy for the second reaction becomes 110 Kj/mol as a result of switching the products and reactants.
2nd - Multiply the second equation by three.
Multiplying the second equation by 3 will get rid of the C terms and will also produce all of the correct number coefficients. The enthalpy for the first reaction remains the same while the enthalpy for the second reaction is multiplied by 3 which results in an enthalpy value of 330 Kj/mol.
3rd - Add the two equations and their enthalpy values together.
The resulting enthalpy value is 354 Kj/mol.
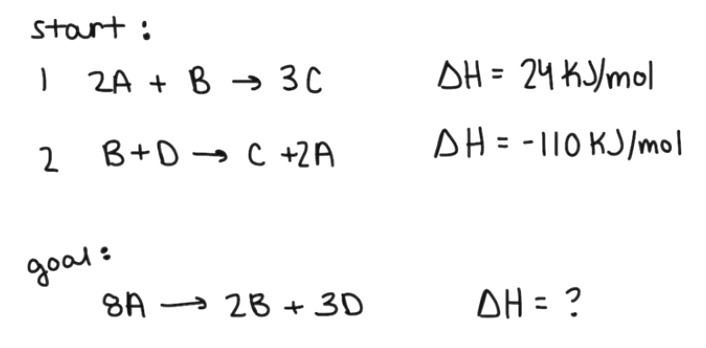
I hope you've found this post about Hess' Law helpful. If you have any questions feel free to comment on this post, message me, or comment on my youtube video below.
- Saren

Helpful Links:





Comments